When a metal is subjected to the perturbation of an octahedral field, the energies of the d-orbitals split into two groups, the lower energy t2g, at -0.4Δo, and the higher energy eg, at 0.6Δo, where Δo is the ligand field splitting parameter.
When electrons are put into these orbitals, the orbitals which become occupied depend on the value of Δo. When there are x electrons in the t2g orbitals, and y electrons in the eg orbitals, the total energy of the electrons relative to the average energy of the electrons is known as the Ligand Field Stabilization Energy (LFSE):
LFSE = (-0.4x + 0.6y)ΔDo
The LFSE therefore depends on the number of electrons in the d-orbitals of the metal, x+y, the value of Δo, and the distribution of electrons between the t2g and eg levels.
When calculating the electronic configuration of a transition metal complex, we should note that the electrons always occupy the lowest energy configuration.
| Electronic Configurations of d-metal complexes | ||
| d1: |  |
t2g1:LFSE = -0.4Δo |
| d2: | 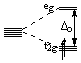 |
t2g2:LFSE = -0.8Δo |
| d3: |  |
t2g3:LFSE = -1.2Δo |
| d4: |  |
t2g4:LFSE = -1.6Δo |
| d4: |  |
t2g3eg1:LFSE = -0.6Δo |
As we can see, when the number of d-electrons is 0, 1, 2, or 3, there is no trouble assigning an electronic configuration, it being t2gn. However, when a 4th electron is added, there are two possible configurations: t2g4 and t2g3eg1. These two configurations differ in LFSE by Δo, and so it would be predicted that the t2g4 configuration would be lower in energy. However, this configuration involves the pairing of electrons in one of the t2g orbitals, and the extra repulsion associated with paired electrons, with energy P, in the same orbital acts to destabilize the t2g4 configuration.
We need to consider the overall stabilization energy, SE, which is the ligand field stabilization energy, LFSE, plus the pairing energy, PE.
| Overall stabilization energy of a d4 complex | |
| t2g4: | SE = LFSE + PE = -1.6Δo + P |
| t2g3eg1: | SE = LFSE + PE = -0.6Δo + 0 = -1.6Δo + Δo |
The configuration adopted therefore depends upon the relative magnitude of the splitting parameter, Δo, and the pairing energy, P. If Δo<P, then the upper eg orbital is occupied to minimize the pairing energy, whereas if Δo>P, the lower t2g orbital is occupied to maximize the LFSE. P does not change, for a given element, and so the configuration is determined by the value of Δo. The first situation, with configuration t2g3eg1 is known as the weak-field limit, and the second, with configuration t2g4, is known as the strong-field limit.
If we consider the MO diagrams for the two d4 complexes, we see that in the weak-field limit, all the electron spins are parallel, and the overall electron spin is 2 In the strong-field limit, two of the electrons are paired, and hence have antiparallel spins, so the overall electron spin is 1. When there is a choice of possible electronic configurations, the configuration with the lowest number of parallel electron spins is known as the low-spin configuration, and it corresponds to the strong field, and the configuration with the highest number of parallel electron spins is known at the high-spin configuration, and it corresponds to the weak-field limit.
Similar arguments can be constructed for d5, d6, and d7 complexes, but for d8, d9, and d10, there is again only one possible configuration.
Ligand field transitions occur when an electron is excited from an orbital with one energy to an orbital with another energy. One example is the t2g-to-eg transition from which the LFSE, Δo, may be calculated. These will sometimes involve a change in the electron spin, and hence have an effect on the magnetic properties if the complex: the magnetic properties of the complex are determined by the number of unpaired electrons.