The name of the group to which a molecule belongs is determined by the symmetry elements it possesses. Grouping together molecules with the same symmetry elements will automatically group together molecules of the same shape eg CX₄ where X = H, F, Cl, Br or I; as long as the four X groups are identical, these molecules will all fall into the same point group. The various point groups are as follows:

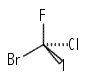
C₁: Molecules which possess only the identity operation. eg CBrClFI , a carbon atom with four different halogens substituted onto it:

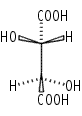
C_i: Molecules with the identity and inversion alone. This is a relatively uncommon point group to encounter in symmetry studies.e.g 

C_s: Molecules with the identity and a mirror plane alone. Again, this is not a commonly encountered point group. e.g:

C_n: Molecules with the identity and a C_n axis alone. Another of the rarely-met point groups. A simple example is hydrogen peroxide, H₂O₂ , which belongs to C₂: 

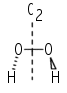
C_nv: Molecules with the identity, a C_n axis, and n vertical mirror planes, σ_v. Commonly encountered examples are water, which belongs to C_2v , and ammonia, which belongs to C_3v. A special subset of this group is the group C_∞v. The group notation implies that all rotations around the axis and reflections in a plane containing the axis are symmetry operations. The group C_∞v consists, therefore, of all linear molecules that do not have a centre of inversion, for example heteronuclear diatomics and the linear OCS molecule

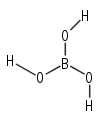
C_nh: Molecules with the identity, a C_n principle axis, and a horizontal mirror plane. e.g. B(OH)₃ , in the correct conformation belongs to C_3h:

D_n: Molecules with the identity, an n-fold principle axis and n C₂ axes perpendicular to the C_n axis.

D_nh: Molecules with the identity,  an n-fold principle axis, n perpendicular C₂ axes, and a horizontal mirror plane. Planar trigonal molecules such as the BX₃ series belong to D_3h , while benzene belongs to the group D_6h. There is a subset of this group, D_∞h , which contains all linear molecules which do have a centre of inversion, for example homonuclear diatomics and ethyne (C₂H₂).

D_nd: Molecules with the identity, an n-fold principle axis, n C₂ axes perpendicular to the C_n axis, and n dihedral mirror planes (vertical mirror planes which bisect the C₂ axes). Allene, H₂C=C=CH₂ , belongs to D_2d: 

S_n: Molecules that do not classify into one of the above groups, but do possess an S_n axis, belong to the group S_n. Molecules in this group with n > 4 are very rare. Note there is no S₂ group, as the S₂ operation is equivalent to an inversion. Thus a molecule that would appear to belong to S₂ is classified as C_i.

Though there are examples of molecules available for all the above groups, naturally some will be encountered more often than others. Those likely to be encountered most often in studies of symmetry are C_nv , D_nh and D_nd. However, one should always be alert to the existence of the other groups, and the possibility that a molecule might classify into one of them instead.

The cubic groups, T, T_d , T_h , O, O_h , I , I_h: These groups all have high symmetry. They are distinguished from the above groups by having no principle axis, but multiple equivalent C_n axes with the highest number of n.
The group T_d is the group of the regular tetrahedron (so would include molecules such as methane, CH₄). The group T contains objects with the rotational symmetry of a tetrahedron but none of its mirror planes, while T_h is based upon the T group but contains an inversion centre. O_h is the group of a regular octahedron (so would contain molecules such as SF₆). O has the rotational symmetry of the octahedron but no mirror planes. The icosahedral group I_h has the symmetry of an icosahedron, and contains the molecule C₆₀, as well as some of the more complex hydrides of boron.
In practice, only the groups T_d , O_h , and I_h are likely to be encountered with any frequency.

The full rotation group, R₃. Contains an infinite number of rotational axes with all possible values of n. This is the point group of a sphere or an atom.

No molecules belong to this group.

It should be noted that the presence of certain symmetry elements automatically indicates the presence of others. For example, an S₂ axis implies the presence of an inversion centre, as the two operations are equivalent. A C₄ axis must also be a C₂ axis, as the C₂ rotation is equivalent to two successive C₄ rotations. Numerous similar examples exist.

Classification of molecules into their point groups is usually achieved with some kind of key or flow diagram which must be followed through answering questions about the symmetry elements an object or molecule possesses, until a classification is made. There are various different charts available for this purpose, an example is given on the next page.