To discuss the thermodynamic properties of liquid mixtures, it is necessary to establish how the chemical potential of a liquid varies with its composition. To calculate the value of the chemical potential of the liquid we use the fact that at equilibrium the chemical potentials of a substance in its liquid and vapour phases are identical.

It is necessary at this stage to specify that quantities relating to pure substances will be labeled with a * i.e. the chemical potential of a pure substance A is written μ_A*.

We know that the chemical potential of a perfect gas at pressure p can be written μ = μº + RT ln (p/pº) , and since the vapour pressure of the pure liquid is p_A* it follows that the chemical potential of A in the vapour phase, which at equilibrium is equal to the chemical potential of the liquid phase, is given by the following expression:  μ_A*  =  μ_Aº  +  RT ln (p_A*/pº)
If there is a solute present in the liquid, then the chemical potential of A in the liquid is μ_A, and the vapour pressure is p_A. Thus, by analogy with the pure liquid situation, we may write: μ_A  =  μ_Aº  +  RT ln (p_A/pº). These two equations may be combined to give:

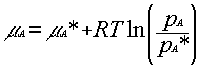
which relates the chemical potential of the pure substance to the chemical potential of the impure substance.

We now use the empirical result known as Raoult's Law: The law states that the ratio of the partial vapour pressure of a liquid in a mixture to the vapour pressure of the pure liquid is approximately equal to the mole fraction of the liquid in the mixture. i.e:

The law indicates that for a mixture of two components, this diagram of vapour pressure against composition should be obtained:

Some mixtures obey Raoult's Law very well, especially if the components of the mixture are structurally similar. Mixtures which obey the law at all compositions, from pure A to pure B, are called ideal solutions. From the previous two equations, we may derive the following expression for an ideal solution:

This equation may now be used as the definition of an ideal solution. i.e. an ideal solution is one which obeys this equation at all compositions. Note that this definition does not require us to assume the vapour is perfect. Further, this definition of an ideal solution rather than being based upon Raoult's Law now implies it instead.

Some solutions show very significant deviations from Raoult's Law, but even in these cases, agreement becomes closer for the component in excess (which we usually identify as the solvent) as it approaches complete purity. i.e. Raoult's Law is usually applicable to the solvent in a dilute solution.