We treat the molecules as hard spheres (of diameter d) - like pool balls. For two molecules to collide, their centres must come within a distance d of each other.

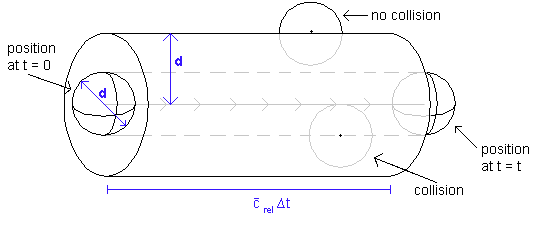
The collision frequency is defined as the number of collisions per unit time. To obtain it, we consider all molecules except one in the sample to be fixed. The one molecule that is in motion moves with speed c_rel (which is defined as the speed of a molecule relative to all the others, ie with all the others being stationary. See below for further details). Now, in a time t, the molecule moves a distance c_relt, and sweeps out a cylindrical path of cross section pd². It follows that the volume of the cylinder swept out by the molecule is sc_relt, where by convention s = pd² and is called the collision cross-section.

The number of stationary molecules with centres inside the cylindrical tube is given by the volume of the tube multiplied by the number of molecules per unit volume in the sample. This latter quantity is known as the number density and is simply N/V (the number of molecules in the sample divided by the volume occupied the sample).

Thus far, we have calculated that the number of molecules with centres inside the tube swept out by the moving molecule is given by πd²tc_relN/V. This is, by definition, the number of collisions made by the moving molecule in a time t. To obtain the number of collisions per unit time, we merely have to divide this quantity by the time, t.

The result (confirmed experimentally) is that z = πd²c_relN/V

Since N = nN_A , (n the number of moles of gas present, N_A Avogadro's number)

N/V = nN_A/ V = pN_A/ RT = p/kT (using pV = nRT)

Thus in terms of pressure, z = pd²c_relp/kt

What is c_rel?

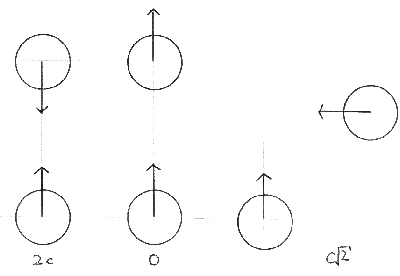
When we are considering collisions between molecules, we are interested in their relative speeds, that is, how fast one is travelling with respect to the other.
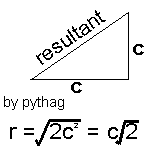Firstly we must assume that all the molecules are all travelling at the mean speed, c.  In the case where they are directly headed for each other, crel = 2c, however, only very few collisions occur like this. Conversely, when both molecules are headed in the same direction, crel = 0. By far and away the majority of collisions occur somewhere inbetween these two extremes. We will summarize these "inbetweens" by considering the 2 molecules as hitting each other at right angles to each other, and simple trigonometry shows that crel = cÖ2.

Hence we can modify our equation (again) to z = pd²cÖ2p/kt, where c is the mean speed of molecules in the sample.