Most atoms are made up of a nucleus surrounded by Z electrons, where Z, the atomic number, is the charge on the nucleus. The forces in these many-electron atoms include the electrostatic attraction between the electrons and the nucleus, but also electrostatic repulsion between the electrons.
The hydrogen atom is special in that it contains only one electron, so its structure is determined only be the attraction between that electron and the nucleus. Other one electron species, such as He+ or C5+, can be described in the same way.
The structure of many electron atoms is described in terms of the structure of the hydrogen atom, with additional terms which allow for the repulsive interaction between the electrons.
The Spectrum of Hydrogen
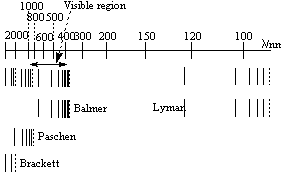
When the atomic emission spectrum of hydrogen is measured, for example by considering the frequencies emitted by the sun, signals at specific frequencies are observed. These correspond to the energy of transitions between the different energy levels that the electron can occupy. The spectrum is below:
The energy of a transition is given by the formula ![]()
, where the transition corresponds to an electron moving from the n1 level to the n2 level. The constant, RH, in this expression is known as the Rydberg Constant, where the subscript H denotes that it is the value for the hydrogen atom. Its value is 13.60 eV (or 1312 kJmol-1).
There are different series corresponding to a different initial energy level, ie: a different value of n1, n2 remains being the final energy level of the electron. They are named after their corresponing discoverers:
| n1 = 1 | Lyman Series (Ultra Violet) |
| n1 = 2 | Balmer Series (Visible) |
| n1 = 3 | Paschen Series (Infra Red) |
| n1 = 4 | Brackett Series (Infra Red) |
The Rydberg constant for hydrogen is the energy of the transition from the n1 = 1 ground state level to n2 = infinity, and corresponds to the ionization energy (removal of an electron from the ground state configuration). Hence, the ionization energy of hydrogen is equal to RH.
The full set of levels n1 and n2 correspond to solutions of the Schrodinger equation for the hydrogen atom, and are known as atomic orbitals. Each atomic orbital can be described by a wavefunction, Ψ(x,y,z), which depends on the electronic coordinates, (x,y,z). According to the Born interpretation of the wavefunction, [Ψ(x,y,z)]2 is the probability of finding an electron near the point (x,y,z).