Carbon has electronic configuration [He]2s22p2, and main formal oxidation state +4 (there are other oxidation states, but all use all of carbon’s valence electrons in bonding).
Alongside the central role of Carbon in Organic Chemistry, it forms numerous compounds, both inorganic and organometallic.
There are two main isotopes, with relative abundances: 12C (98.9%, I=0), and 13C (1.1%, I=0.5). I is the nuclear spin, and the half-integer value of the nuclear spin for 13C gives it its usefulness in structure determination by NMR.
Elemental carbon occurs in several different forms, ie. it displays a complex allotropy. The main forms are diamond and graphite, and they exhibit markedly different properties due to the very different structures they adopt.
Structures and Descriptions
| Diamond | ||
| An electrical insulator, and 3D-lattice crystal structure. This is the hardest known substance (this is because it is made up of very strong C-C covalent bonds). Each C atom forms four bonds, tetrahedrally arranged, to other C atoms, resulting in an open, but strongly bonded, 3D-structure. |  |
Diamond (Cubic): 4-coordinate, sp3 tetrahedral carbon coordination. |
| Graphite | ||
| An electrical conductor, and layered lattice crystal structure. This is slippery and used as a lubricant (this is a property of its layered structure, with the lubricating effect coming from the ability of the layers to slide over one another, as they are only weakly held together by van der Waals forces). Here, each C atom forms three covalent σ-bonds to further C atoms. These σ-bonds are made up of sp2 hybrid orbitals. The remaining p-orbitals, which are perpendicular to the plane of the σ-bonds, overlap to form a delocalized π-system. The planes are widely separated as they are held together only by the weak van der Waals forces. |  |
Graphite (hexagonal): 3-coordinate, sp2 planar carbon coordination. the lines show that the carbon atoms in every other layer are in line, and notthose in adjacent layers. |
Diamond does not convert to graphite under standard conditions, even though it is spontaneous (ΔGo = -2.90 kJmol-1). This is a kinetic phenomenon, and diamond is thus described as metastable.
The electrical conductivity of graphite is direction-dependent: the π-system of delocalized electrons allows metallic conduction parallel to the planes, while the much lower conductivity perpendicular to the planes, which nevertheless increases with temperature, suggests semiconductor behavior in that direction.
The directionality of the conductivity suggests a band structure of graphite which has a fully filled valence band with a small separation to the empty conduction band (the overlapping p-orbitals, with one electron from each C atom, form a π-system with the bonding orbitals fully occupied and the anti-bonding orbitals fully unoccupied. Hence, graphite may form intercalation compounds with species which act either as electron donors (where graphite acts as an electron acceptor, incorporating the donated electrons into the vacant conduction band), or as electron acceptors (where graphite now donates electrons from the full valence band).
Reactions of Graphite
| Reduction by K (extra electrons from the K enter the graphite conduction band, and therefore increase conductivity) |
| Oxidation by Br (electrons from the graphite valence band are lost to form Br anions, leaving holes in the graphite band which therefore increase the conducivity) |
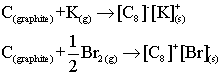 |
| With F; produces (CF)n, an electrical insulator, which has a structure resembling continuous fused cyclohexane rings, containing sp3 hybridised C atoms. |
Fullerenes
If sheets of Graphite were bent, which in practice is achieved by replacing some of the six-membered rings by five-membered rings, then other forms of carbon may be formed. These are known as fullerenes (so named after the inventor of the geodesic dome, Buckminster Fuller; the domes have the similar shapes to these compounds), or Bucky-balls. In practice, they are formed when an electric arc is struck across graphite electrodes in an inert atmosphere.
The most important of these is C60, often referred to as Buckminster-Fullerene but others such as C70, C76 and C84 occur in smaller quantities.
- C60: an individual C60 molecule has the shape of a soccer-ball, and Ih (icosahedral) symmetry. Each pentagon is surrounded by hexagons, and each hexagon is surrounded by three pentagons and three hexagons. It crystallizes to give a magenta solid, and dissolves in benzene to give a magenta solution. The 13C NMR spectrum shows one signal, ie. all the C atoms in C60 are equivalent.
- C70: this has the structure of C60 with an extra strip of five hexagons around the center of the soccer-ball. It crystallizes to give a red-brown solid, and dissolves in benzene to give a red solution. The 13C NMR spectrum shows five signals, so C70 contains C atoms in five different environments.
| Structure of C60 | |
 |
 |
| Plan view, looking down the C5 axis. | The bonds between sp2hybridised carbon atoms make up the familiar shape of a football, and the pentagons and hexagons can be seen. |
Reactions of Fullerenes:
The reactivity of fullerenes is somewhere between that of an arene (with an extended graphite like p-system) and an alkene (with an isolated C=C double bond).
The addition product with K is a superconductor below 18K, whose structure is an face centered cubic array of C60 molecules, with K+ ions occupying all the octahedral and tetrahedral holes; the product with OsO4 is a standard alkene-like addition, where the OsO4 adds across a C=C bond. The reaction with Na and NH3 is known as the Birch reduction.
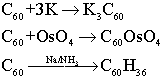
Nanotubes:
If a C60 molecule is split in half, the two hemispheres can be placed on the ends of a rolled-up sheet of graphite to produce what is known as a nanotube. Many different sizes of tube may be formed, capped or uncapped by bucky-balls of different sizes, and these may have huge future technological use as molecular wires, as they retain some of the conductivity of the parent graphite.